SSL常用于网站的通信，是现代通信中最常用的加密方案，那么SSL，或者说是非对称加密算法究竟是如何实现的呢？
如何证明我是我？
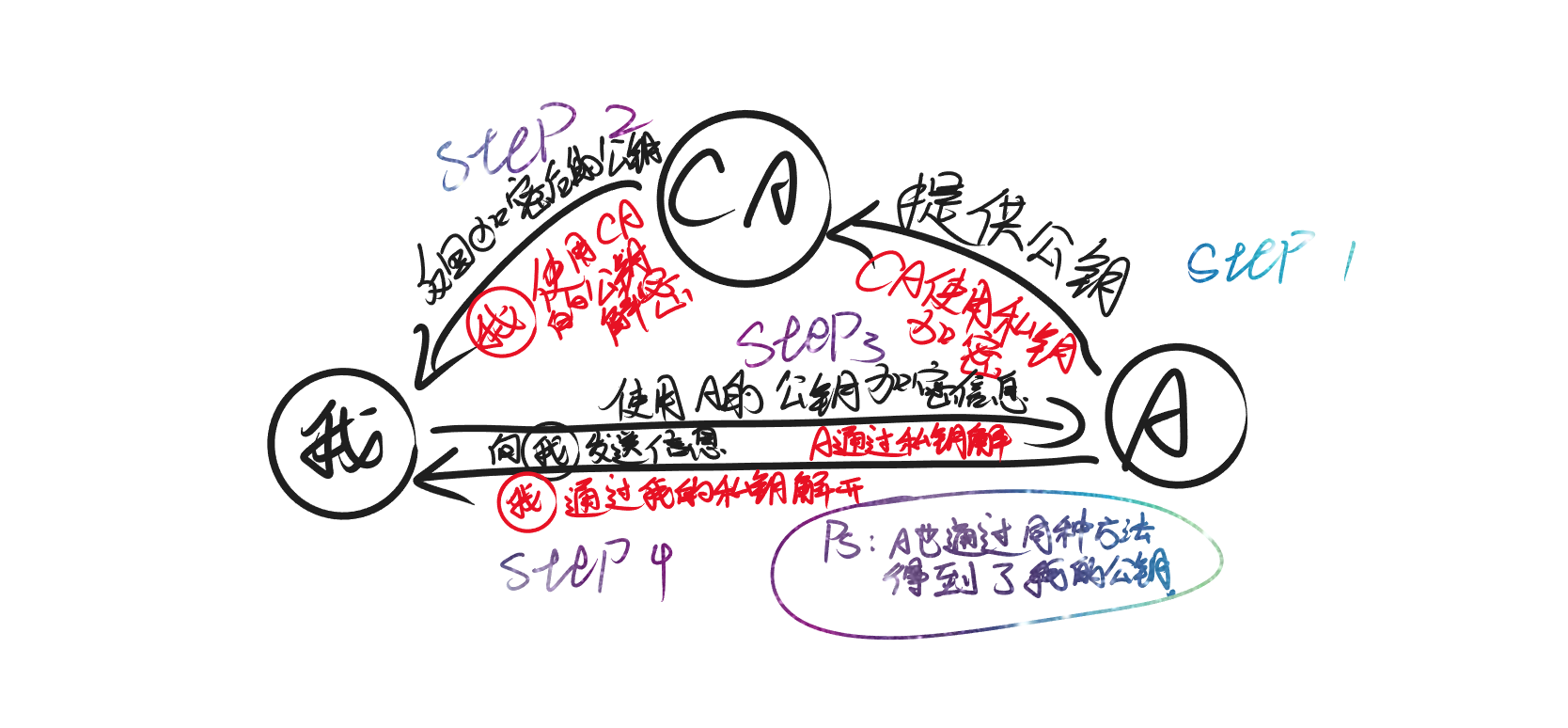
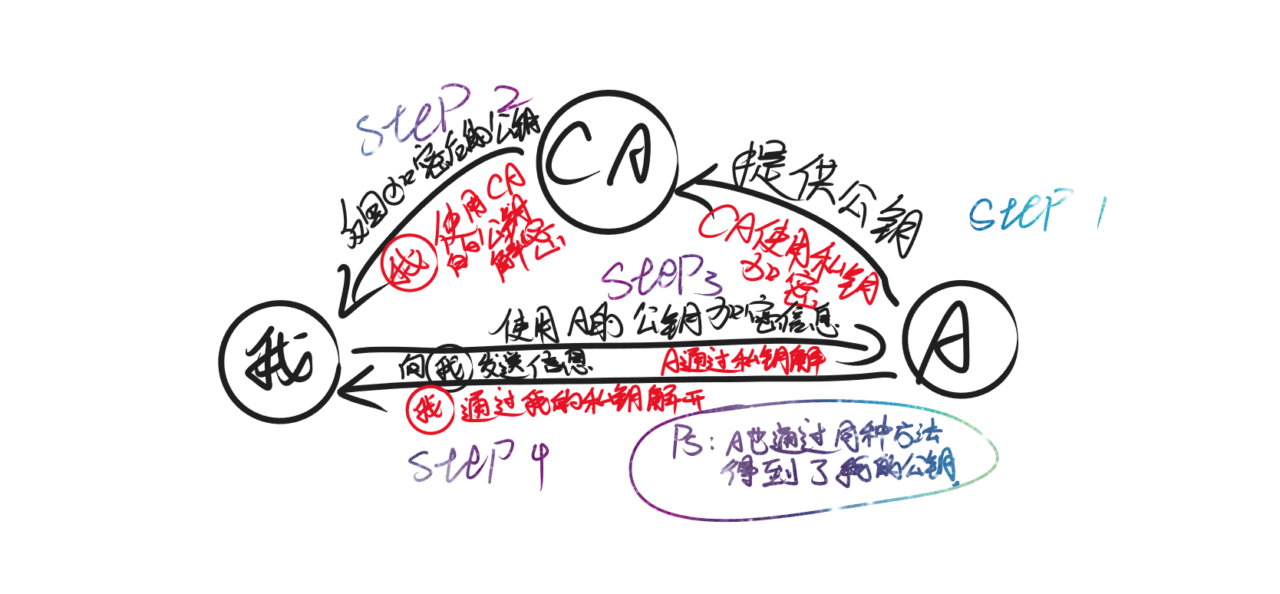
在发送信息的时候，我们通常需要证明我是我，而在信息世界中，这一步同样存在在信息世界中，我们通常会通过信任一个CA机构来完成这一步，这里需要引入一个概念公钥和私钥，顾名思义，公钥是公开给所有人的一把钥匙，它能够解开你使用私钥加密的内容，私钥则是你自己所使用的，CA机构同样也会拥有公钥和私钥，CA机构使用私钥加密A的公钥并告诉我，我再通过CA机构的公钥解开，我因为信任CA机构，所以我信任这个公钥是A的公钥，因此对方也能通过相同的方法来确认我是我。
内容交换的流程？
在证明了我是我以后，我们就可以来传输数据了，下面的步骤就简单了，我通过公钥加密内容发送给A，A通过私钥解密，再通过私钥加密回复我的信息。
非对称加密（RSA）算法是如何实现的？
数论中有一个理论
每个大于1的自然数，要么本身就是质数，要么可以写作多个质数的积，且写法只有一个。
这里不得不提到一个数学概念，质数。任何一个偶数是都可以写成几个质因数相乘的形式，且结果只有一个，如3,458就可以写作下面的几个质数相乘。
2X7X13X19
在上边的例子中3458就是公钥2 7 13 19这几个数字就是私钥，我们知道3458，但却很难推断出它是 2 7 13 19这几个数相乘，知道了这些，我们只要设置一个足够复杂的数字，就足以做到加密。
非对称加密能够被破解吗？
有的人发现，我们可以用枚举法来找到一个合数所对应的几个质数，这样不就可以破解非对称加密算法了嘛。
真的吗？
我在上面说到，我们需要一个足够复杂的公钥，人类分解质因数的能力是很弱的，哪怕使用电脑，你依旧需要花费大量的时间来枚举，这几乎是不可能被寻找出来的（欧皇除外）。如果你不相信，欢迎挑战RSA在1978提出的这一道考题，尝试分解出组成它的质数。
114381625757888867669235779976146612010218296721242362562842935706935245733897830597123563958705058989075147599290026879543541这个数字，人们花了17年才解了出来，而它只有178个数字。你会发现，想要把一个很大的数做质因数分解实在是太难了。而在现实中，加密算法所使用的数字只会比它更长，更加难以计算。
一个很有意思的发现
如果认真看完这一篇文章，你会发现，我们很难知道这些质数是多少，但是我们可以很容易的知道别人算出来的质数是对还是错，我们只需要验证所有乘数是质数，再验证乘积就可以知道是对还是错。
非对称加密可以被破解吗？
可以，也不可以。
这并不矛盾，可以指的是你知道破解它的方法，你也能够成功；不可以则是你无法实现这样的操作，仅仅178个数字就花费了人们17年，而现在网络交易所使用的RSA-2048有617个数字，如今这个算法被悬赏20万美金来对它进行分解。
Finally found a platform that actually delivers on its promises. The game variety is impressive and I had a great experience with the support team. Highly recommend krmegawins
I appreciate how steady and reliable this corner of the web has been for me lately. The betting markets are wide and the odds actually make sense without any sketchy adjustments behind the scenes. It really is a comfort zone whenever I need a trusted place to enjoy my downtime. mo88bet
[3794]Crazy Time অফিসিয়াল লগইন | বিকাশ পেমেন্ট ও ক্যাসিনো বোনাস,Crazy Time অ্যাপ ডাউনলোড করে সেরা অনলাইন ক্যাসিনো বোনাস বুঝে নিন। বিকাশ পেমেন্ট গেটওয়েতে দ্রুত লেনদেন ও স্লট গেমের নিয়ম জানুন। আজই জয়েন করুন। visit: crazy time
Really impressive variety of games available here. I spent hours exploring different options and everything works perfectly. bd6777bat is definitely my new go to spot.
赞一个
量子计算机出现会使得基于质因数分解的加密的枚举破解时间降低几个量级
大胆想象一下1145141919810位的加密算法